高校生になってから2次関数がわかりづらくなった人いませんか?
おそらくその理由は、高校生で習う2次関数は動きが複雑だからではないでしょうか。(中学ではグラフの中に図形が存在したり、その面積を求めたりと、違った意味で難しいかもしれませんが、、、)
実際に中学で習う2次関数は、基本的には原点に頂点が存在するものを習います。それが高校では、頂点が原点にあるとは限りません。
そのため、2次関数のグラフの方程式が複雑だったりします。
今回は、それを「GeoGebra」を使って、式のどの部分がどのように対応しているのかを見ていこうと思います。
はじめに
今回、最後まで見ていただけたら、2次関数のグラフの平行移動の単元が感覚的に身につくようになっています。
是非、一緒に「Geogebra」を使ってグラフを描きながら勉強していってください。
GeoGebraってなに?
そもそも「GeoGebra」とは何かというと、数学や科学を小学校から大学水準まで学習指導するための動的な数学ソフトウェアです。
実際にパソコンの検索画面で「GeoGebra」と検索してみてもらった方がわかりやすいです。
まあ、グラフを描いたりいろんなことができるソフトということで構いません。
今回はこれを使って2次関数をいろいろ動かしてみます。
実際に使ってみる
まずはこの画面になると思いますので↓赤枠ののとこをクリックしましょう♪
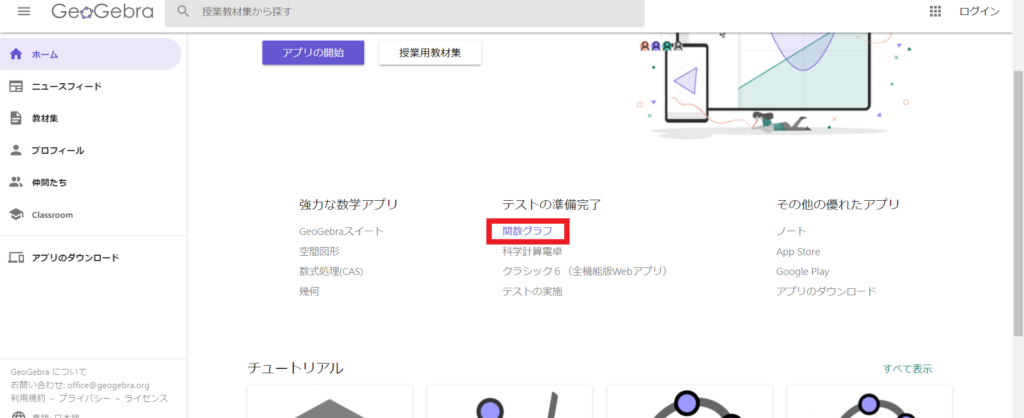
そしたらグラフを描く画面になりますので、まずは適当にグラフを入力して遊んじゃいましょう♪
さて、ここからが本題です。
以下の赤枠に関数を入力するのですが、今回は、まず
$$y=ax^2$$
と入力してみてください。↓このように「a」はそのまま入力してください。
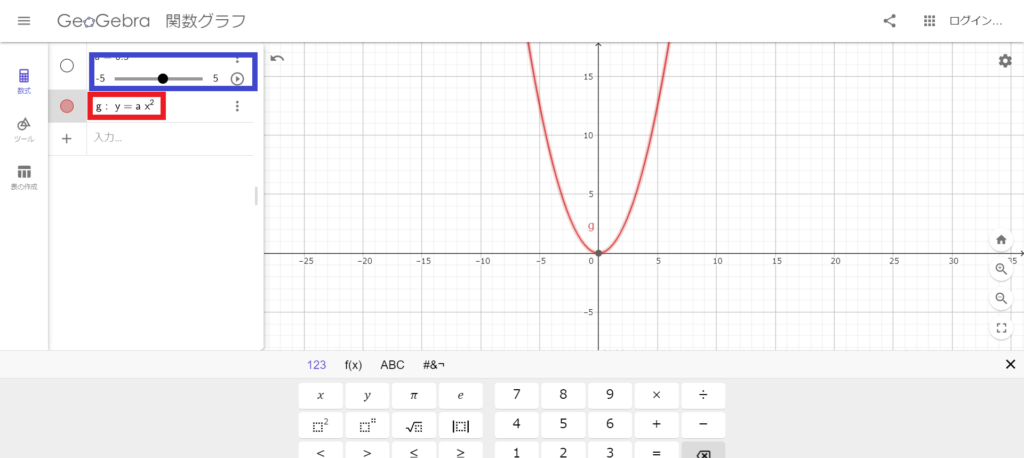
赤枠のところに関数を入力すると、「a」と入力した部分を青枠のところで動かすことができます。「再生ボタン」をクリックすると自動で動かすこともできます。
実際に動かしてみると、グラフの「向きやひらき具合」が変化する様子が観察できたと思います。(ここまでは中学内容)
つぎに、同じ要領で
$$y=2(x-a)^2$$
と入力してみましょう。今回は、\(x^2\)の係数は適当に固定して(今回は2に固定してみます)動かしてみましょう。
どうだったでしょうか?
2次関数の式の\(x\)の部分が\(x-a\)に変えたら、グラフ上ではグラフが左右に動いたはずです。

また、\(a=5\)のところでちょうど止めてみてください。頂点の\(x\)座標がちょうど「5」のところで止まっているのがわかります。
そうです。今回\(a\)で置いた部分は頂点の\(x\)座標を表す場所だったのです。
では次に、これを入力してみてください。
$$y=2(x-5)^2+a$$
今度も\(x^2\)の係数は2に固定して、頂点の\(x\)座標は5で固定して調べてみましょう。
何が変わりましたか?今度は上下に移動したはずです。

今度は\(a=3\)のところで止めてみました。よくみると頂点の\(y\)座標が「3」のところで止まっているのがわかります。
そうです。今回、\(a\)で置いた部分は頂点の\(y\)座標を表す場所だったのです。
これらのことを踏まえると次のことが言えそうです。
グラフを動かしてみてわかること
2次関数
$$y=a(x-p)^2+q$$
において、頂点は(\(p,q\))となり、\(a\)は向きやグラフの開き具合に関係する。
また\(x\)が\(x-p\)に代わるとグラフは\(x\)軸方向に\(p\)だけ移動し、
$$y-q=a(x-p)^2$$
\(q\)を左辺に移項して式変形したものを考えてみると、\(y\)が\(y-q\)に代わるとグラフは\(y\)軸方向に\(q\)だけ移動することがわかる。
まとめ
今回、「GeoGebra」というソフトを使って、グラフの動きを確認していきました。
教科書の表の変化とグラフの様子をリンクさせるのは、教科書を見るだけでは大変です。実際にグラフを動かしてみることによって、何が変化するのかを観察できたりするので、皆さんもいろんなグラフを描いてみてください。
数学Ⅲの内容では、マクローリン展開(実際には大学内容)などを書いてみると実際の近似の様子がすごくよくわかると思いますので、是非、使ってみて遊んでみましょう♪


コメント