今回は高次方程式方程式でよく使われる「解と係数の関係」についてじっくりと説明していきます。
では、早速
2次方程式の解と係数の関係
解と係数の関係ってなんだ?
って思いますよね。実は数学でよく使う計算テクニックの一つなんです。
本来、2次方程式の解は「解の公式」を使えばすべて求まります(虚数解も含む)。
しかし、高次方程式の単元では複素数の範囲で解を求めるため、
解をそのまま扱うと式が煩雑になることが多いので、
「解の和」や「解の積」を使って計算を簡単にしようと試みます。
なので、あくまでも「計算法(テクニック)」なんです。
それでは、説明に移ります。2種類の方法で説明しますが、解と係数の関係を忘れたけどサクッと思い出したいって時には、一つ目の方法をおススメします。
まず大前提として、
2次方程式は一般的に解を2つもちます(重解も含みます)。このとき、2つの解をαとβとします。
まず、2次方程式
$$ax^2+bx+c=0・・・①$$
を準備します。もちろん2次方程式なので、\(a\)は0ではないとします。
解と係数の関係の求め方①
①の式の両辺を\(a\)で割ります。
そうすると、式はややこしくなりますが、
$$x^2+\frac{b}{a}x+\frac{c}{a}=0・・・②$$
という式が出てきます。
また、①の式はαとβを解に持つことから、
$$(x-α)(x-β)=0$$
の式が成立します。この式の左辺を展開すると
$$x^2-(α+β)x+αβ=0・・・③$$
となります。②の式と③の式はともに、αとβを解に持つ2次方程式であり、左辺の\(x^2\)の係数が一致することから、
左辺の\(x\)の係数や定数項(\(x\)がついていない項)も一致します。
よって、
\(x\)の係数について、\(-(α+β)=\frac{b}{a}\)つまり\(α+β=-\frac{b}{a}\)が成立し、
定数項について、\(αβ=\frac{c}{a}\)が成立します。
解と係数の求め方②
①の式について解の公式を使って解きます。
$$x=\frac{-b±\sqrt{b^2-4ac}}{2a}$$
という2つの解が出てきます。これら2つの解がαとβなので、「和」と「積」を実際に求めてみます。
まずは「和」から、
$$α+β=\frac{-b-\sqrt{b^2-4ac}}{2a}+\frac{-b+\sqrt{b^2-4ac}}{2a}=-\frac{b}{a}$$
分子のルートの部分が相殺されて、きれいになりました。次は、「積」
$$αβ=\frac{-b-\sqrt{b^2-4ac}}{2a}・\frac{-b+\sqrt{b^2-4ac}}{2a}=\frac{(-b)^2-(b^2-4ac)}{4a^2}=\frac{c}{a}$$
ちょっと面倒ですが、なんとか計算できました。
公式(解と係数の関係)
$$ax^2+bx+c=0$$
について、
$$α+β=-\frac{b}{a}$$
$$αβ=\frac{c}{a}$$
が成立する。
注意事項
注意事項が2つあります。
1つ目は、2次方程式でしか利用できないということです。
そりゃそうだろうと思うかもしれませんが、意外と3次方程式なのに使おうとしてしまう人がいるので気を付けてください。
2つ目(これが重要!!)、解と係数の関係は
解がわからないから使うのではなく煩雑になるから計算をラクにするために使います。
実際に、解の公式を使えば、解は求まります。
なぜ、強調したかといいますと、以下の問題を見てください。
例)
$$x^2+3x-4=0の解をαとβとおくとき、2α+βの値を求めよ。$$
どうですか?解と係数を使おうとすれば困難ですよね。
解の公式または因数分解を使えば、2通りの答えが一瞬で出ます。
\(α+β\)と\(αβ\)のみの式になるのは、「対称式」です。
「対称式」とはαとβの位置を入れ替えても同じ式です。
例えば、\(α^2+β^2\) の式のαとβの位置を入れ替えたとして \(β^2+α^2\) なので、同じ式になりますよね。
\((β-α)^2\)とかもそうです。
解と係数の関係が使いづらいときには実際に解の公式を使って計算をしていくことを忘れないようにしましょう。
おまけ(解と係数の関係を使って問題に挑戦してみよう)
放物線 \(y=x^2+x-6\) を直線 \(y=2x\) の交点をA、Bとおく。線分ABの長さを求めよ。
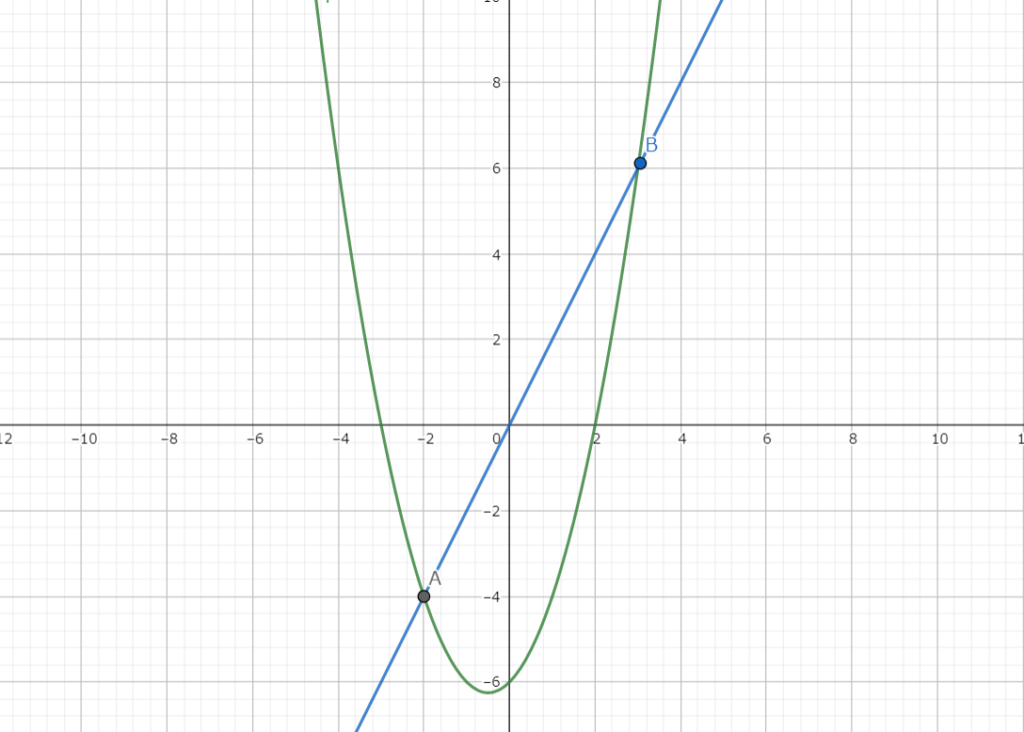
どうですか?共有点の\(x\)座標と\(y\)座標を求めて、三平方の定理を使っても出ますが、、、
今回あえて解と係数の関係を使ってみます。
まず、共有点の\(x\)座標のみに注目します。
二つの関数をつなげて
$$x^2+x-6=2x$$
式変形をして
\(x^2-x-6=0\)の解をαとβとして、解と係数の関係をつかうと
$$α+β=1 , αβ=-6$$
となります。ここで\(β-α\)を計算します。(\(α<β\)とする)
$$(β-α)^2=(α+β)^2-4αβ=1+24=25$$
よって
$$β-α=5$$
となります。これは以下の図の①の長さが求まったことになります。
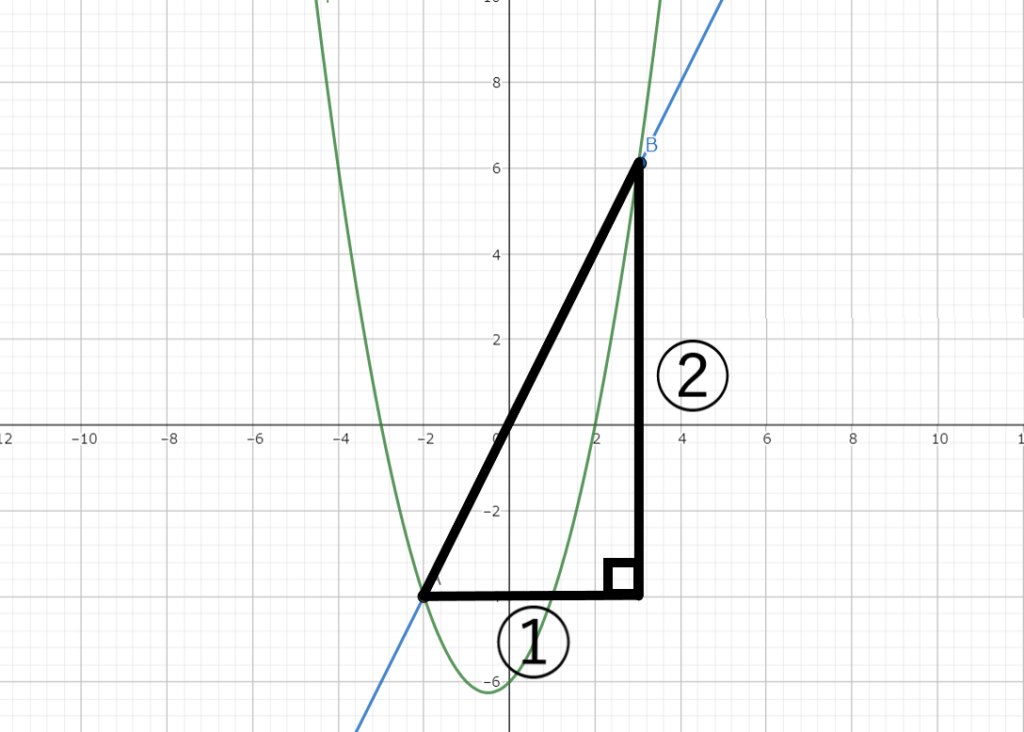
直線の傾きが2なので横の長さと縦の長さの比が1:2の直角三角形を考えます。
ここで斜辺は横の長さの\(\sqrt{5}\)倍の大きさになるので、
線分ABの長さは\(5\sqrt{5}\)となります。
どうでしょうか?
実際に切り取る線分の長さを求めるときには「解と係数の関係」をよく使います。
最後に・・・
皆さんお疲れ様でした。
今回、高次方程式でよく出てくる「解と係数の関係」についてじっくり説明してみました。
解と係数の関係は計算テクニックとして、いろいろな場面で活躍してきます。
しかし、「解と係数の関係」が使えない場面でも、解は求まる!ということを意識しておくことも忘れないようにしておきましょう。



コメント