さて今回は高校数学で初登場の絶対値の「場合分け」にチャレンジしてみましょう。
「場合分け」といわれたら、なんか色々あって複雑そう・・・
てなイメージがあると思うのですが、実際には真逆で
複雑なものを分けて考える(困難は分割せよ!byデカルト)ことによって簡単に考えられるようにしよう!
ということなんです。
どうですか?少し「やってみようかな?」ってなりましたか?
はじめに
初めに、絶対値とは「原点からの距離」です。ここで難しいと思った人は、「距離」だけに注目しましょう。
「距離」と言われれば、必ず0以上の値を取りそうだということがわかるでしょう。
そうなんです。絶対値は必ず0以上の値なんです。
例えば\(|-2|=2\)のように。
詳しく言えば、0から\(-2\)までの距離が「2」だけ離れているということなんです。
絶対値の外し方(その1)中学での外し方
さて、絶対値はそのまま計算することは、ほぼありません。
ほとんどの場合、絶対値を外してから計算を行います。(もちろん例外もあります)
それでは、実際に絶対値を外してみましょう。
ここでは中学校で習ったルールを使って外しましょう(復習)。
$$|-5|=5$$
$$|3|=3$$
$$|3|+|-5|=3+5=8$$
どうですか?3つともできましたか?
ルールの確認ですが、ここでは、マイナスがついていた数字に関してはマイナスをのけて外し、プラスの数についてはそのまま外しました。
もちろん正解です!!!(パチパチ)
ちゃんと外せましたね。ではなぜ高校数学になったら難しく感じるのでしょうか?見ていきましょう。
絶対値の外し方(その2)高校での外し方
実は、高校での絶対値の外し方は中学の外し方とは少し違います。
え???って思った人は、ココを乗り切れば絶対値なんて「ただの縦棒」にみえますよ!
ではいきますよ~♪
高校では・・・
$$|-5|=-(-5)=5$$
です!
なんと!!・・・一緒ではないか?って思った人!
高校では「マイナスのものはマイナスを付けて外す」のです。プラスの時の外し方は同じなので、省略しますが、これが実はものすご~く大事なのです。
高校では、数字を扱うより文字を扱うことが多いので、例えば\(a\)といわれてもこの\(a\)がプラスのものなのかマイナスのものなのかがわからないのです。
ココで考えてみましょう!\(a\)がマイナスの数なら\(|a|\)はどうやって外しますか?
中学までなら、マイナスが見えていたので、マイナスをのけてやれば外せました。
今回は\(a\)がマイナスの数なので、マイナスが見えません。
どうする?どうする?
「マイナスを付けて、プラスの状態にして外す」
これです!
絶対値の外し方(その3)文字が入った場合
その2までの内容を踏まえて、文字が入ったときの絶対値を外してみましょう♪
\(|a|\)に関して
(ⅰ)\(a≧0\)の場合、\(|a|=a\) (\(a\)がプラスなのでそのまま外す)
(ⅱ)\(a≦0\)の場合、\(|a|=-a\) (\(a\)がマイナスなのでマイナスを付けて外す)
です。ここで大事なのは、「絶対値を外した後は必ずプラスの状態である」ということです。
(ⅱ)の時なんて、ぱっと見ただけでは\(-a\)でマイナスがあるから、マイナスっぽいような見た目ですが、本当はプラスなんですね~。
中学との違いが、分かってきましたでしょうか?
練習問題
さて、実際に問題を解いてみましょう。
$$|x-1|=2x$$
(まずは、絶対値がついている状態では計算できないから、、、)「外そう!!」
(ⅰ)\(x-1≧0\)つまり\(x≧1\)のとき
\(x-1=2x\)・・・(そのまま外しました)
\(x=-1\)・・・(\(x\)について解きました)
\(x=-1\)は条件に当てはまらないので不適当。・・・(場合分けの範囲に入っていないので残念ながら答えになりません。)
(ⅱ)\(x-1≦0\)つまり\(x≦1\)のとき
\(-(x-1)=2x\)・・・(絶対値の中身がマイナスの数なので、マイナスを付けて外しました)
\(-x+1=2x\)より\(3x=1\)
\(x=\frac{1}{3}\)・・・(\(x\)について解きました)
\(x=\frac{1}{3}\)は条件を満たす・・・(場合分けの条件にしっかり当てはまります。)
(ⅰ)(ⅱ)より\(x=\frac{1}{3}\)・・・(最後に結果を書きます。完成!)
グラフによる考察(おまけ)
少しだけ、グラフでも考えてみましょう。
今回の絶対値の問題は、実は・・・
\(y=|x-1|\)のグラフと\(y=2x\)のグラフの共有点の\(x\)座標を求めていることと同じなんです。
なので、実際にグラフ作成ソフトで確認してみましょう♪
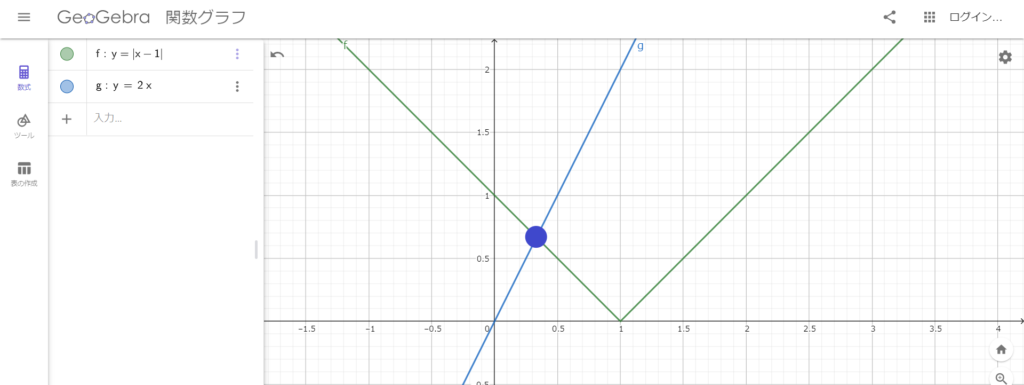
Geogebraというソフトで書いてみました。
\(x=\frac{1}{3}\)のところあたりで交わっているように見えます。
最後に・・・
どうだったでしょうか?ちゃんと最後まで解ききれましたか?
高校に入って初めての場合分けです。お疲れさまでした。これで絶対値マスターですね♪
今回、「中学で習った絶対値の外し方」と「高校で習った絶対値の外し方」の違いに着目して説明しました。
実際にはもう少し計算がハードなものもありますが、基本的な考え方は同じです。
理解できたら、持っている問題集などでどんどん練習してみましょう♪
きっと解けるようになっていますよ。



コメント